前言

我曾经在 MaTeX 与 LaTeX 一文中提到过谢尔宾斯基三角形，当时是用 上下标的方式巧妙构造出来的：

Rotate[MaTeX[Nest[StringReplace[#,"\\circ"->"{\\circ}^{\\circ}_{\\circ}"]&,"\\circ",5],FontSize->6,Magnification->2],270Degree]

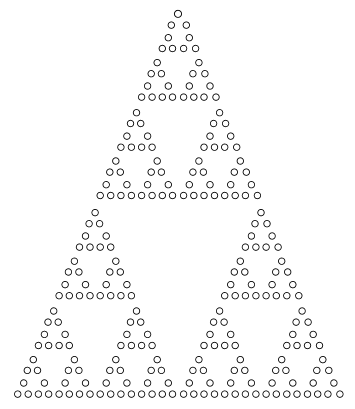
这次，我们探讨谢尔宾斯基三角形的其他绘制方法（时隔 1 年，终于填坑了）

根据原理进行区分，主要介绍 3 种绘图方法：

• 对图形的迭代（迭代替换法）
• 对函数的迭代（迭代函数系统）
• 对字符串的迭代（Lindenmayer 系统）

谢尔宾斯基三角形

在 Mathematica 用下面一行代码即可画出谢尔宾斯基三角形，长这个样子：

对图形的迭代

本方法的原理是：

1. 取一个实心的三角形（多数使用等边三角形）
2. 连接三边的中点，将它分成四个小三角形
3. 去掉中间的小三角形
4. 对其余三个小三角形重复步骤 2

这个过程的示意图：

代码：

GraphicsGrid[Partition[Table[Graphics@{EdgeForm[Black],Nest[Translate[Scale[#,0.5,{0,0}],CirclePoints[0.5,3]]&,Triangle@CirclePoints[3],n]},{n,0,8}],3],Frame->All]

对函数的迭代

”函数“指的是迭代函数系统，迭代函数系统将待生成的图像看做是由许多与整体相似的（或经过一定变换后与整体相似的）小块拼贴而成，比如：

（捅了猫窝了）

---

然后介绍仿射变换 。以二维图形为例，如下的仿射变换

它可以把下面的左图变换成右图：

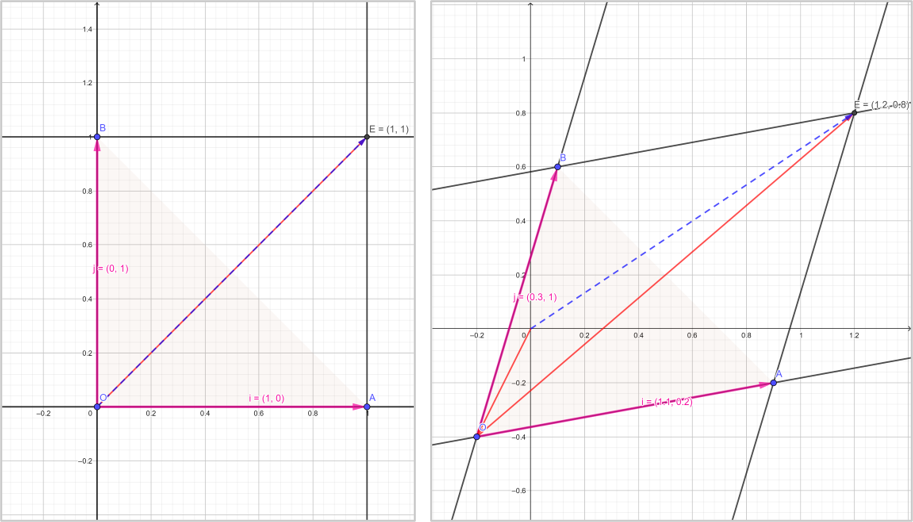
其实就是线性变换再平移。那么上文对图形的迭代就可以用仿射变换来描述：

---

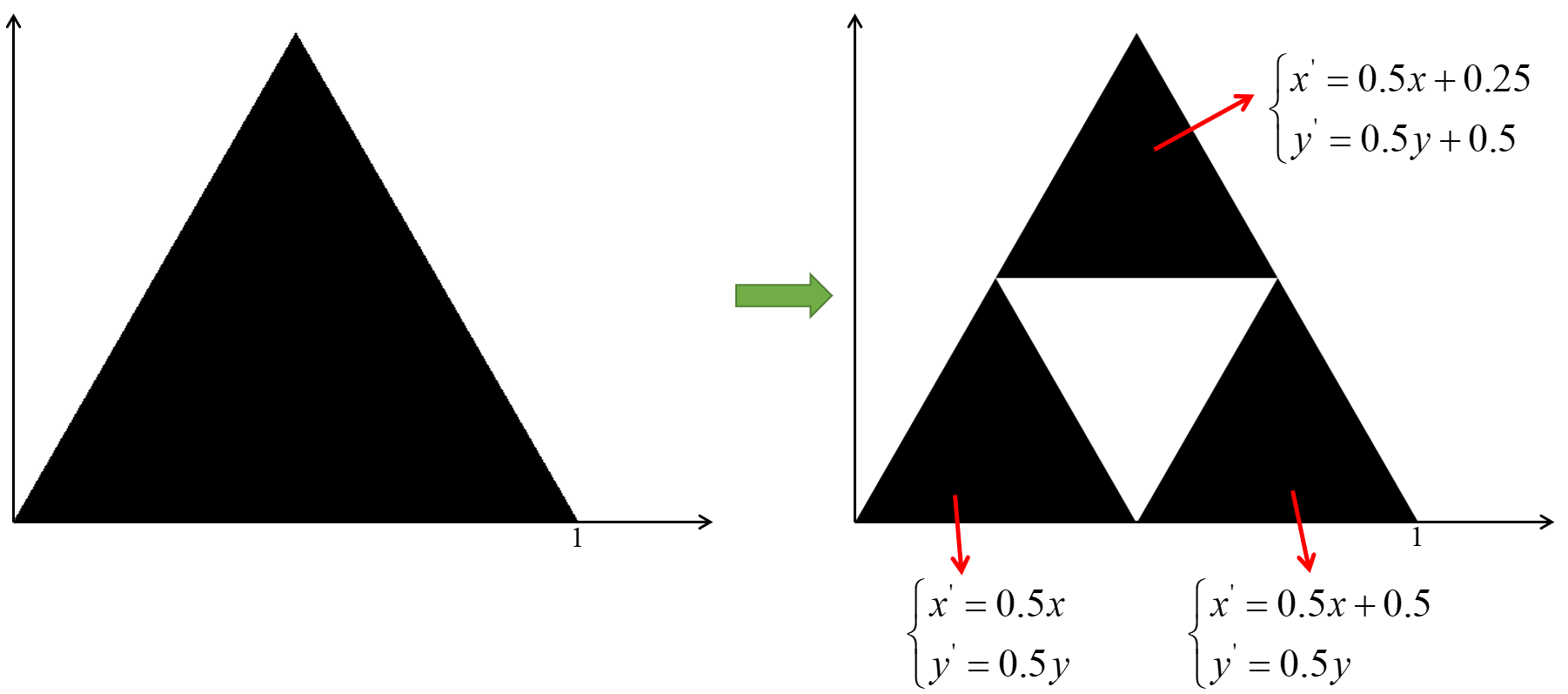
本方法的原理是：

对一个初始图形以相等的概率随机使用上图的 3 个变换，得到的图形再重复这个过程

这个过程的示意图：

代码：

AffineTrans=AffineTransform[{0.5IdentityMatrix[2],#}]&/@{{0,0},{0.5,0},{0.25,0.5}};
GraphicsGrid[Partition[Table[Graphics[{PointSize@Tiny,Point@NestList[(RandomChoice@AffineTrans)[#]&,{0,0},2^(n+6)]}],{n,1,9}],3],Frame->All]

对字符串的迭代

Lindenmayer 系统，又称 L 系统、林氏系统。是一种字符串重写系统。

字符串重写：根据语法规则对所给字符串进行迭代生成新字符串，每次迭代的结果称为一代。

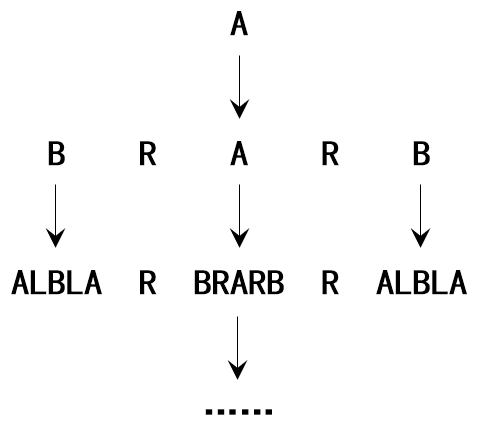
Mathematica 里也有相关的函数：

字符串解释：将字符串中的字符解释为适当的几何元素，就可以得到一个基于语法规则生成的图形。

---

本方法的示意图：

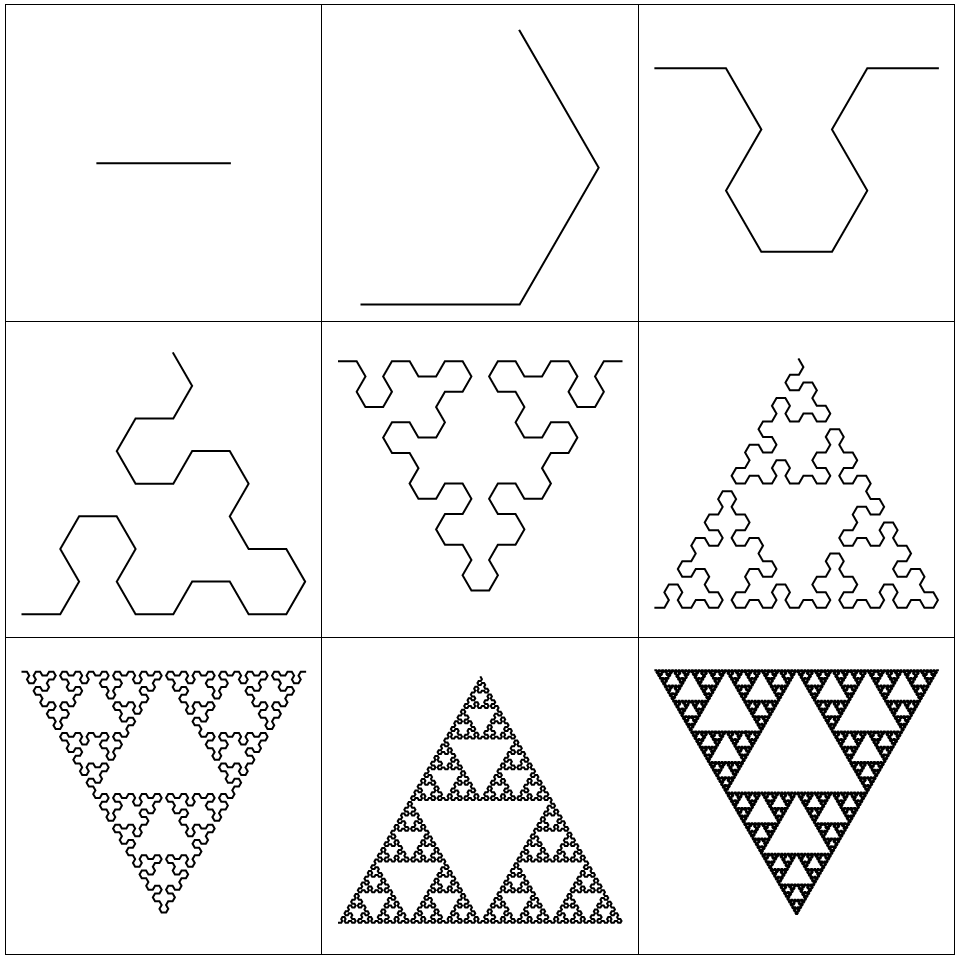
代码如下：

forward[{z_,a_}]:={z+E^(I a),a};
left[{z_,a_}]:={z,a+Pi/3};
right[{z_,a_}]:={z,a-Pi/3};
GraphicsGrid[Partition[Table[ComplexListPlot[First/@Split[First/@ComposeList[Flatten@Nest[#/.{A->{B,R,A,R,B},B->{A,L,B,L,A}}&,A,n]/.{A->forward,B->forward,L->left,R->right},{0,0}]],Joined->True,PlotStyle->Black,Axes->False],{n,1,9}],3],Frame->All]

还有一种更短小精悍的写法：

GraphicsGrid[Partition[Table[Graphics@Line@AnglePath[Pi/3 Nest[Flatten@{-#,1,#,1,-#}&,0,n]],{n,1,9}],3],Frame->All]